Permutation test 和 Oster test 的 Stata 实现
置换检验和 Oster test 的 Stata 实现
后文用的模型均为:
$$
y_{it} = \beta_0 + \beta_1x_{it}+\beta’ controls_{it} + \mu_i + \lambda_t + \epsilon_{it}
$$
内生性问题主要包括遗漏变量、反向因果还有选择性偏误,第一个问题可以通过增加更多变量解决,比如引入其他层面的固定效应,第二个反向因果问题可以通过工具变量法等方法解决,第三个选择性偏差包括样本选择偏误和自选择偏误,前者可以通过 PSM-DID 等方法解决,后者可以通过Heckman 2sls 等方法解决。本文介绍的Permutation test 和 Oster test 是从另外一个视角去探讨遗漏变量内生性问题,尤其是在找不到工具变量和遗漏变量不可观测、不可分离的时候较为有效。
1 Permutation test / Randomization test / 置换检验
排除共存事件的影响,比如在做 DID 的时候,有些其他事件冲击可能与我们所关心的事件是同时发生的,通过置换检验一定程度上可以排除这些共存事件的干扰。
1 | reg y x age size soe i.industry i.year, r |
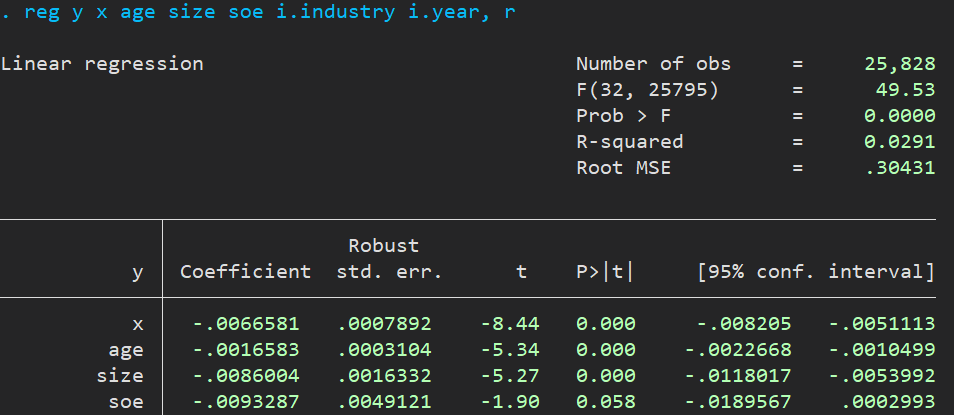
接下来的是对 $x$ 进行 permute 500 次【命令中的 permute x 和 option 里面的 reps(500) 】,每次都是对同一家公司不同年份进行 permute 【option 里面的 strata(code)】,这样就不会把 A 公司的数据给了 B 公司(不然就搞得和安慰剂检验差不多了)。最终的目的是对 x 的系数进行估计【命令中的 beta=_b[x] ,意思就是把 x 的系数赋值给 beta 这个变量名,其实改成别的或者不加也行】,冒号后面是基准模型。
1 | permute x beta=_b[x], reps(500) strata(code):reg y x age size soe, r |
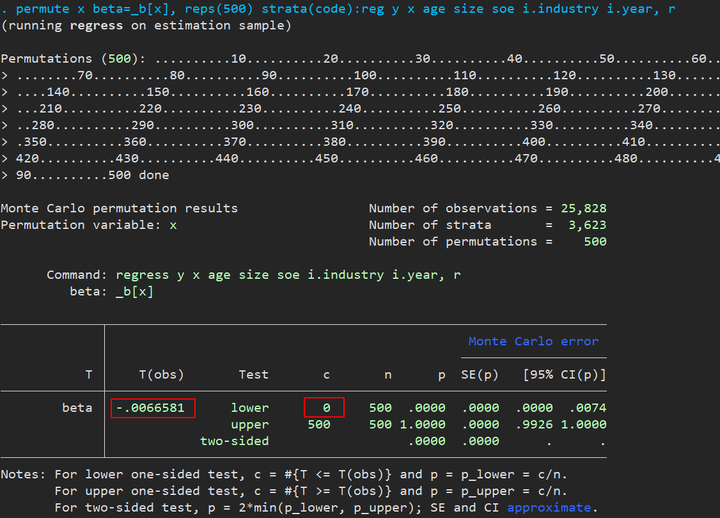
图中的 -0.0066581 就是前面基准回归的系数,由于这个系数是负的,所以我们看看这 500 次里面有多少次是比这个系数更负,也就是 lower 后面那个数字 0 ,意思就是 500 次 permute 的结果,$x$ 的系数全都大于 -0.0066581,经验 $p$ 值为后面的 0.0000(计算方法是 p = c / n),说明我们的结果是稳健的,不太可能有共存的事件影响我们的估计结果。
tips:如果原本的系数是正的就看下面的 upper 那行
此外,如果做的是 DID 的话,比如方程是
$$
y_{it} = \beta_0 + \beta_1treat_{i}\times post_t+\beta’ controls_{it} + \mu_i + \lambda_t + \epsilon_{it}
$$
那就可以把命令改成对 $treat$ 进行 permute,
1 | permute treat beta=_b[c.treat#c.post], reps(500) strata(code):reg y c.treat#c.post age size soe i.industry i.year, r |
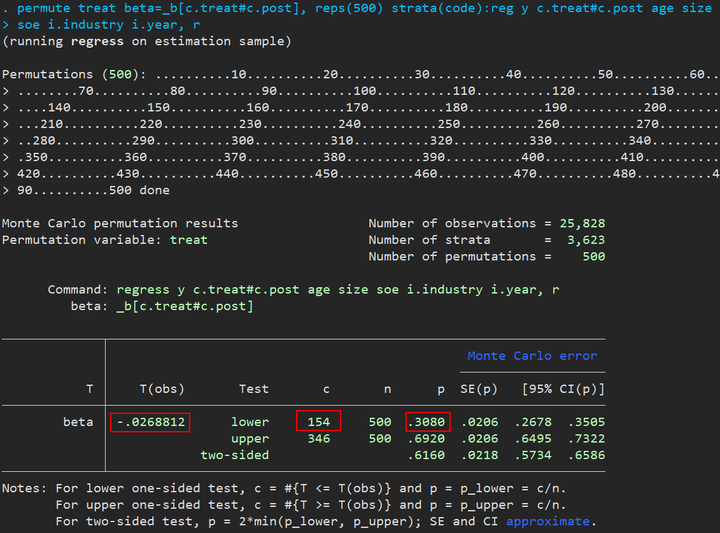
经验 $p$ 值 0.3080 (154 / 500),500 次 permutation 里面就有 154 次比 -0.0268812 要小,所以置换检验没有通过,共存事件的影响不可忽视。
2 Oster test(2019)
其实这个检验目前还没有明确的名字,我姑且叫它 Oster test 吧。这个检验是用来检验遗漏变量的影响,比如,未观测到的因素需要比已观测到的因素作用大多少才能够对原估计结果产生显著影响(使 β = 0 或者 β 逆转为正数[前面提到的结果是负数]),所以这个办法本质上就是用来说明遗漏变量不会影响我们的主要结果。
2.1 是否存在和已经观测到的变量同等重要的未观测到的变量对我们的估计结果产生影响?
更新:建议使用 github 上提供的 psacalc2,支持 reghdfe 命令后果运行,使用方法不变
Oster test 分为两个部分,首先第一个部分是用来检验是否存在和已经观测到的变量(包括固定效应)同等重要的未观测到的变量对我们的估计结果产生影响?
按照 Oster 原文以及一些顶刊的做法,通过 $R^2$ 和 $\delta$ 对“真实的” $\beta$ 区间(true $\beta$)进行复原。首先给出两个假设,
- 引入未观测到的因素后 $R^2$ 会变为原来 1.3 倍(这个 1.3 是 Oster 的建议值);
- 未观测到的变量对被解释变量的影响和已观测到的变量(包括固定效应)的影响至少相同(即 $\delta = 1$ ,也是个建议值)
用到的 Stata 包是 psacalc,执行的命令为
1 | reg y x age big4 dual assets debts top institude soe, r level(99.5) // 置信区间设为 99.5% ,后面有用 |
首先是回归结果,记住这个 99.5 % 置信区间 [-0.0092741, -0.0052753],
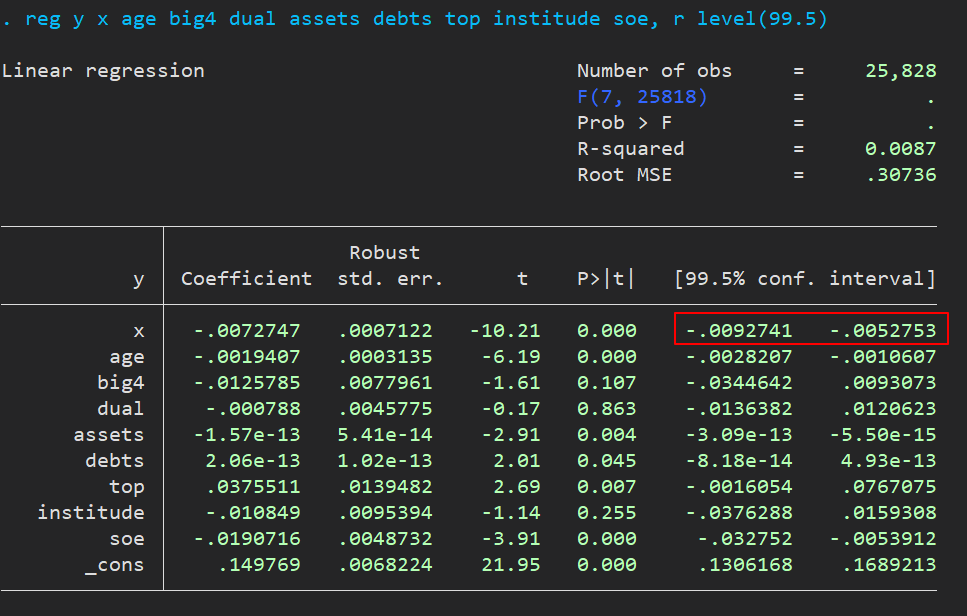
psacalc beta 的输出结果如下,
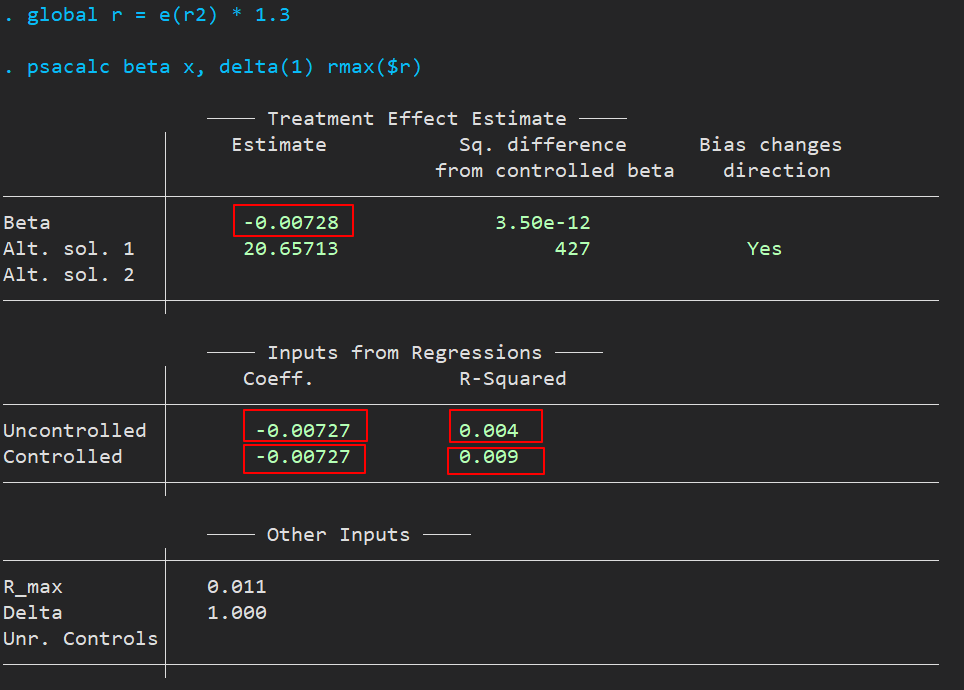
没有引入控制变量和固定效应前,回归系数为 -0.00727 ,对应的 $R^2$ 为 0.004,控制后分别变为 -0.007270(没变,好家伙,为了区分多加个 0) 和 0.009,上面有个 beta 值为 -0.00728,
那么上面汇报的 beta 值与控制后的系数组成了“真实的” $\beta$ 区间 [-0.00728, -0.007270],该区间不包含 0 值,且落于前面提到的 99.5% 置信区间 [-0.0092741, -0.0052753] 内。这个结果说明了不太可能与已经观测到的变量(包括固定效应)同等重要的未观测到的变量对我们的结果产生显著影响。(使得 $\beta$ 失效等于 0 或令其逆转为正)
2.2 未观测到的变量至少要产生多少倍于已经观测到的变量的影响才能够使得 β = 0?
第二个检验换了一个角度去思考,假设
- 引入未观测到的因素后 $R^2$ 会变为原来 1.3 倍(这个 1.3 是 Oster 的建议值);
- $\beta = 0$
执行的命令为
1 | psacalc delta x, beta(0) rmax($r) |
结果输出如下,
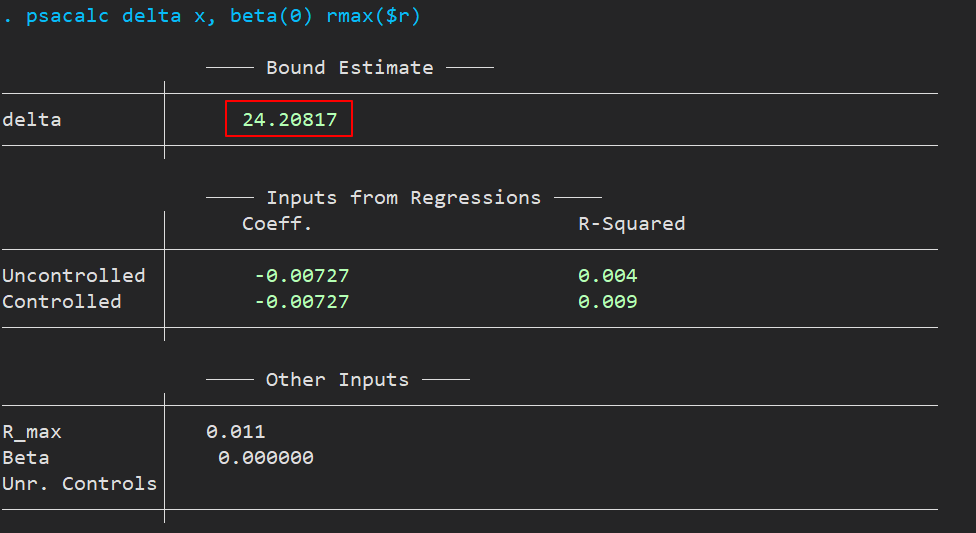
可以发现上面的 delta 值为 24.20817 ,也就是说,未观测到的变量产生的影响至少24倍于已经观测到的变量才能够使得 β = 0,该结果表明不太可能存在未观测到的变量对我们的结果产生显著影响。(存在24倍影响的未观测变量是不太可能的)
根据知乎评论区朋友提供的资料,下面这个链接认为 delta 小于 0 时,只要小于 -1 也是可以的。
==> 知乎文章
我在其他的论文中发现 delta 其实小于 0 都是可以的,说明加入遗漏变量后,系数会更偏向于基准的方向。
3 怎么汇报结果?
那么 Oster test 的结果应该如何汇报呢?我找了下文献,看到有这两种汇报方法,
- Donohoe, M.P., Jang, H. and Lisowsky, P., 2022. Competitive externalities of tax cuts. Journal of Accounting Research, 60(1), pp.201-259.

- Aubery, F. and Sahn, D.E., 2021. Cognitive achievement production in Madagascar: a value-added model approach. Education Economics, 29(6), pp.670-699.
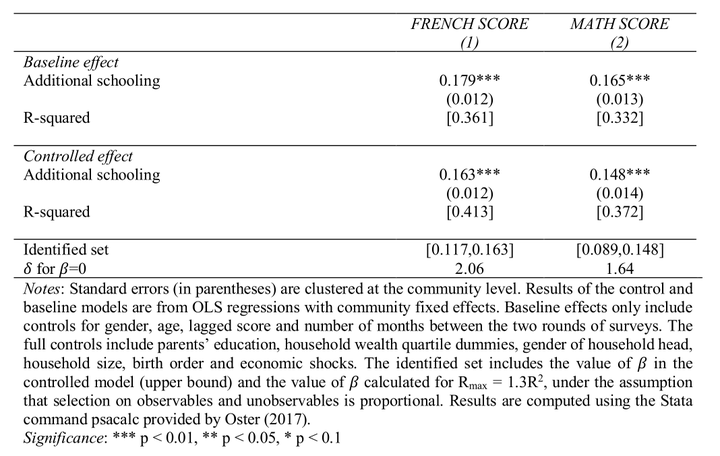
顺带加个置换检验的展示图,
- Donohoe, M.P., Jang, H. and Lisowsky, P., 2022. Competitive externalities of tax cuts. Journal of Accounting Research, 60(1), pp.201-259.
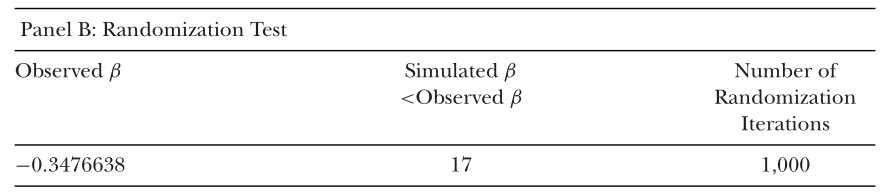
如有不对还请指出!
4 参考资料
Permutation test 和 Oster test 的 Stata 实现