堆叠双重差分模型
发表更新编程学习6 分钟读完 (大约874个字)0次访问

堆叠双重差分模型

堆叠双重差分模型方法

1 堆叠DID（stacked DID）和多期DID（staggered DID）的区别

1.1 Difference in data

  • Setting

Sample windows: 2001 - 2005

Adoption year stkcd Group type
1999 1 Always treated
2002 2 Early treated
2004 3 Late treated
. 4 Never treated
  • Staggered DID panel data (N = 4 $\times$ 5 = 20)
stkcd year y DID Treat Adoption year
1 2001 55 1 1 1999
1 2002 64 1 1 1999
1 2003 21 1 1 1999
1 2004 45 1 1 1999
1 2005 67 1 1 1999
2 2001 82 0 1 2002
2 2002 63 1 1 2002
2 2003 78 1 1 2002
2 2004 99 1 1 2002
2 2005 51 1 1 2002
3 2001 54 0 1 2004
3 2002 36 0 1 2004
3 2003 41 0 1 2004
3 2004 65 1 1 2004
3 2005 94 1 1 2004
4 2001 76 0 0 .
4 2002 37 0 0 .
4 2003 11 0 0 .
4 2004 76 0 0 .
4 2005 44 0 0 .
  • Stacked DID panel data (N = 3 $\times$ 10 = 30)
stkcd year y DID Treat Adoption year in cohort Cohort
1 2001 55 1 1 1999 1
1 2002 64 1 1 1999 1
1 2003 21 1 1 1999 1
1 2004 45 1 1 1999 1
1 2005 67 1 1 1999 1
4 2001 76 0 0 . 1
4 2002 37 0 0 . 1
4 2003 11 0 0 . 1
4 2004 76 0 0 . 1
4 2005 44 0 0 . 1
2 2001 82 0 1 2002 2
2 2002 63 1 1 2002 2
2 2003 78 1 1 2002 2
2 2004 99 1 1 2002 2
2 2005 51 1 1 2002 2
4 2001 76 0 0 . 2
4 2002 37 0 0 . 2
4 2003 11 0 0 . 2
4 2004 76 0 0 . 2
4 2005 44 0 0 . 2
3 2001 54 0 1 2004 3
3 2002 36 0 1 2004 3
3 2003 41 0 1 2004 3
3 2004 65 1 1 2004 3
3 2005 94 1 1 2004 3
4 2001 76 0 0 . 3
4 2002 37 0 0 . 3
4 2003 11 0 0 . 3
4 2004 76 0 0 . 3
4 2005 44 0 0 . 3

1.2 Difference in specification

  • Staggered DID specification

$$
y_{it} = \alpha + \beta DID_{it} + \eta’ Controls_{it} + \delta_{i} + \lambda_{t} + \varepsilon_{it}
$$

where

$y_{it}$ is the outcome variable

$DID_{it}$ is the event dummy variable

$Controls_{it}$ is a vector contains a series of variables

$\delta_i$ and $\lambda_t$ are firm and year fixed effect, respectively

  • Stacked DID
  1. Reduced form

$$
y_{ict} = \alpha + \beta DID_{ict} + \eta’ Controls_{ict} + \delta_{ic} + \lambda_{tc} + \varepsilon_{ict}
$$

where

$c$ is the cohort of firm $i$

$\delta_{ic}$ and $\lambda_{tc}$ are firm-cohort and year-cohort interacted fixed effect, respectively

  1. Event study form

$$
y_{ict} = \alpha + \sum\limits_{
\begin{array}{*{20}{c}}
{- 3 \leqslant k \leqslant 3} \
{k \ne - 1}
\end{array}}
\beta_k Treat_{ic} \times I( t - A_c = k ) + \eta’ Controls_{ict} + \delta_{ic} + \lambda_{tc} + \varepsilon_{ict}
$$

where

$A_c$ is the adoption year of cohort $c$

$I()$ is an indicator function, equaling 1 when the inner equation holds

or more specifically
$$
y_{ict} = \alpha + Before3_{ict} + Before2_{ict} + Currenct_{ict} + After1_{ict} + After2_{ict} + After3_{ict} + \eta’ Controls_{ict} + \delta_{ic} + \lambda_{tc} + \varepsilon_{ict}
$$

2 偏误的来源

  • Two assumption for common trend
    • Time-varying confounders must affect outcomes in both groups in the same way. -> Time fixed effects
    • Group-varying confounders must be time-invariant. -> Group fixed effects

Goodman-Bacon, A. (2021). Difference-in-differences with variation in treatment timing. Journal of Econometrics, 225(2): 254-277.

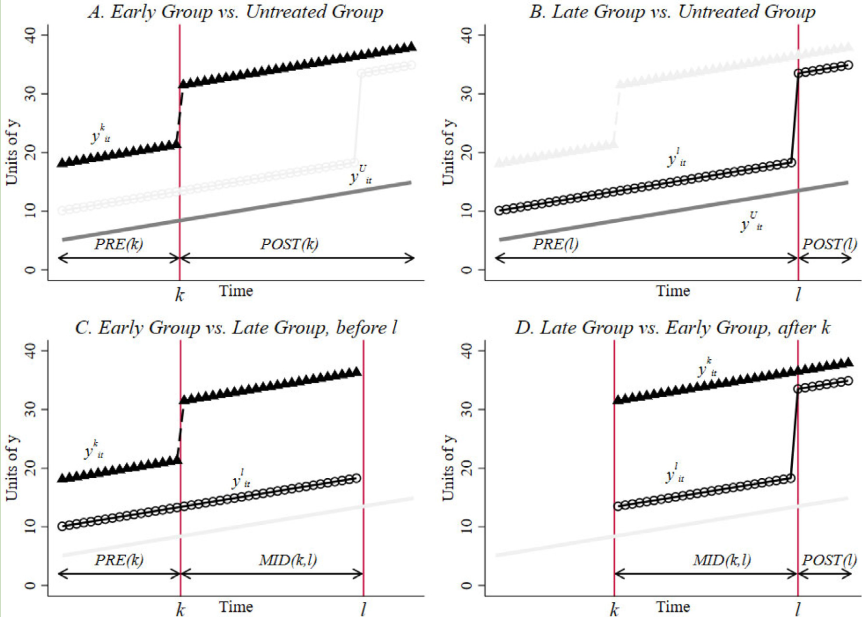
培根分解图

Because the early group (bad control) is treated as a control group

See more details in Staggered Adoption Designs and Stacked DID and Event Studies (Coady Wing, 2021)

3 Stata code

3.1 Staggered DID

  • code
1
2
3
4
5
cd "D:\code\Stata\stackeddid"

use "demo.dta", clear
* Staggered did
reghdfe y did, a(stkcd year) vce(cl stkcd)
  • output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
. reghdfe y did, a(stkcd year) vce(cl stkcd)
(MWFE estimator converged in 2 iterations)

HDFE Linear regression                            Number of obs   =         20
Absorbing 2 HDFE groups                           F(   1,      3) =      17.15
Statistics robust to heteroskedasticity           Prob > F        =     0.0256
                                                  R-squared       =     0.5608
                                                  Adj R-squared   =     0.1656
                                                  Within R-sq.    =     0.0988
Number of clusters (stkcd)   =          4         Root MSE        =    20.9805

                                  (Std. err. adjusted for 4 clusters in stkcd)
------------------------------------------------------------------------------
             |               Robust
           y | Coefficient  std. err.      t    P>|t|     [95% conf. interval]
-------------+----------------------------------------------------------------
         did |   19.26923    4.65359     4.14   0.026     4.459429    34.07903
       _cons |   47.35192   2.559475    18.50   0.000     39.20653    55.49731
------------------------------------------------------------------------------

Absorbed degrees of freedom:
-----------------------------------------------------+
 Absorbed FE | Categories  - Redundant  = Num. Coefs |
-------------+---------------------------------------|
       stkcd |         4           4           0    *|
        year |         5           0           5     |
-----------------------------------------------------+
* = FE nested within cluster; treated as redundant for DoF computation

3.2 Stacked DID

  • code
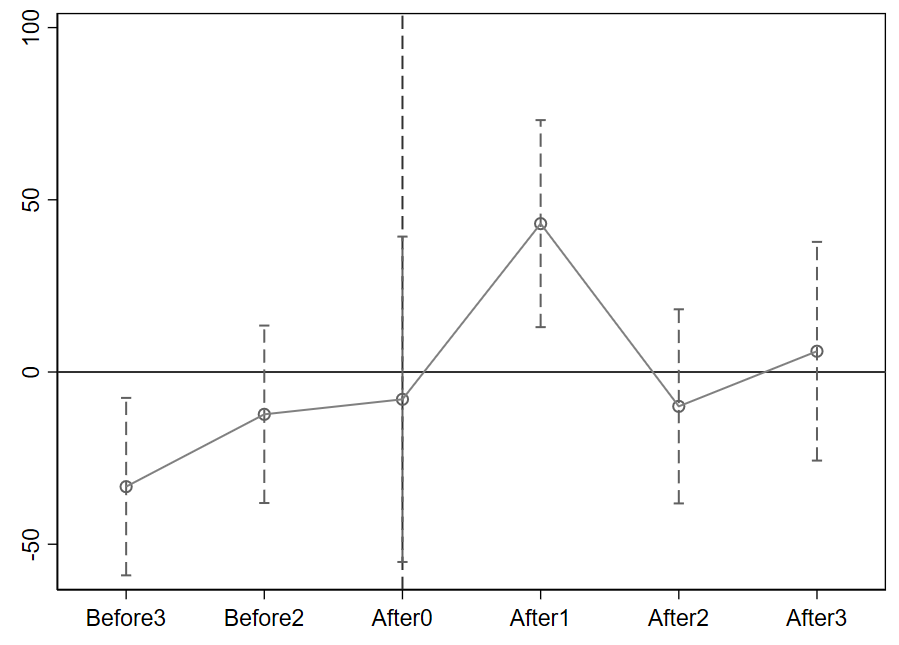
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
cd "D:\code\Stata\stackeddid"

use "demo.dta", clear
* Stacked did
// adoption year = 1999
drop if adoptionyear == 2002
drop if adoptionyear == 2004

gen cohort = 1

save "cohort1.dta", replace

// adoption year = 2002
use "demo.dta", clear

drop if adoptionyear == 1999
drop if adoptionyear == 2004

gen cohort = 2

save "cohort2.dta", replace

// adoption year = 2004
use "demo.dta", clear

drop if adoptionyear == 1999
drop if adoptionyear == 2002

gen cohort = 3

save "cohort3.dta", replace

append using "cohort1.dta"
append using "cohort2.dta"

sort cohort stkcd year
save "stackedmain.dta", replace

reghdfe y did, a(stkcd#cohort year#cohort) vce(cl stkcd)

// event study form
forvalue i = 3(-1)2{
    gen Before`i'_ = cond(year - adoptionyear <= -`i' & adoptionyear != ., 1, 0)
}

forvalue i = 3(-1)1{
    gen Before`i' = cond(year - adoptionyear == -`i', 1, 0)
}

forvalue i = 0(1)3{
    gen After`i' = cond(year - adoptionyear == `i', 1, 0)
}

forvalue i = 2(1)3{
    gen After`i'_ = cond(year - adoptionyear >= `i' & adoptionyear != ., 1, 0)
}


reghdfe y Before3 Before2 After0 After1 After2 After3, a(stkcd#cohort year#cohort) vce(cl stkcd)
est store m1
coefplot m1, keep(Before3 Before2 After0 After1 After2 After3) ///
			 levels(90) ///
			 vertical yline(0) xline(3, lp(dash)) ///
			 addplot(line @b @at) ciopts(lpattern(dash) ///
			 recast(rcap) msize(medium)) ///
			 msymbol(circle_hollow) ///
			 scheme(s1mono)
  • result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
. reghdfe y did, a(stkcd#cohort year#cohort) vce(cl stkcd)
(MWFE estimator converged in 2 iterations)

HDFE Linear regression                            Number of obs   =         30
Absorbing 2 HDFE groups                           F(   1,      3) =      89.20
Statistics robust to heteroskedasticity           Prob > F        =     0.0025
                                                  R-squared       =     0.7619
                                                  Adj R-squared   =     0.1367
                                                  Within R-sq.    =     0.0929
Number of clusters (stkcd)   =          4         Root MSE        =    22.3113

                                  (Std. err. adjusted for 4 clusters in stkcd)
------------------------------------------------------------------------------
             |               Robust
           y | Coefficient  std. err.      t    P>|t|     [95% conf. interval]
-------------+----------------------------------------------------------------
         did |       20.2   2.138754     9.44   0.003     13.39353    27.00647
       _cons |   47.49333   .7842096    60.56   0.000     44.99763    49.98904
------------------------------------------------------------------------------

Absorbed degrees of freedom:
--------------------------------------------------------+
    Absorbed FE | Categories  - Redundant  = Num. Coefs |
----------------+---------------------------------------|
   stkcd#cohort |         6           6           0    *|
    year#cohort |        15           0          15     |
--------------------------------------------------------+
* = FE nested within cluster; treated as redundant for DoF computation

. reghdfe y Before3 Before2 After0 After1 After2 After3, a(stkcd#cohort year#cohort) vce(cl stkcd)
(MWFE estimator converged in 2 iterations)
warning: missing F statistic; dropped variables due to collinearity or too few clusters

HDFE Linear regression                            Number of obs   =         30
Absorbing 2 HDFE groups                           F(   6,      3) =          .
Statistics robust to heteroskedasticity           Prob > F        =          .
                                                  R-squared       =     0.8914
                                                  Adj R-squared   =    -0.0501
                                                  Within R-sq.    =     0.5863
Number of clusters (stkcd)   =          4         Root MSE        =    24.6071

                                  (Std. err. adjusted for 4 clusters in stkcd)
------------------------------------------------------------------------------
             |               Robust
           y | Coefficient  std. err.      t    P>|t|     [95% conf. interval]
-------------+----------------------------------------------------------------
     Before3 |  -33.27778   10.94557    -3.04   0.056    -68.11146    1.555902
     Before2 |  -12.27778   10.94557    -1.12   0.344    -47.11146     22.5559
      After0 |  -7.916667    20.0721    -0.39   0.720    -71.79504    55.96171
      After1 |   43.08333   12.77056     3.37   0.043     2.441714    83.72495
      After2 |  -9.972222   11.97396    -0.83   0.466     -48.0787    28.13425
      After3 |   6.027778   13.48936     0.45   0.685    -36.90138    48.95693
       _cons |   54.33704   3.490034    15.57   0.001     43.23019    65.44388
------------------------------------------------------------------------------

Absorbed degrees of freedom:
--------------------------------------------------------+
    Absorbed FE | Categories  - Redundant  = Num. Coefs |
----------------+---------------------------------------|
   stkcd#cohort |         6           6           0    *|
    year#cohort |        15           0          15     |
--------------------------------------------------------+
* = FE nested within cluster; treated as redundant for DoF computation

平行趋势图

4 参考文献

Chen, Z., Cao, Y., Feng, Z., Lu, M., & Shan, Y. (2023). Broadband infrastructure and stock price crash risk: Evidence from a quasi-natural experiment. Finance Research Letters, 58, 104026. Q2. https://doi.org/10.1016/j.frl.2023.104026

堆叠双重差分模型

https://codefoxs.github.io/2024/04/11/1-堆叠双重差分模型/

作者

CodeFox

发布于

2024-04-11

更新于

2024-06-05

许可协议

#

评论

关注我

链接

分类

标签

GitHub2
Stata8
搜索网站1
数学4
社科基金1
网络加速2
考博2
计量经济学8
金融学2

归档

×