统计学复习

统计学复习，参考书目：

《统计学》第八版：贾俊平、何晓群、金勇进

《统计学导论》第四版：曾五一、肖红叶

1 基本概念

（1）什么是统计学

统计学是收集、处理、分析、解释数据并从数据中得出结论的科学

严格来说不是数学的分支，并且不是独立学科

主要流派包括：政治算术派（威廉·配第）、国势学派（阿亨瓦尔）、社会统计学派（克尼斯）、数理统计学派（凯特勒）：细分为经典学派、贝叶斯学派

（2）统计数据及其类型

• 计量尺度来看

分类数据（定类尺度和定序尺度）、数值型数据（定距尺度和定比尺度）（贾俊平）

数据的尺度包括：定类尺度、定序尺度、定距尺度、定比尺度（曾五一）

• 收集方法来看

观测数据：通过观察或观测收集到的数据

实验数据：在实验中控制实验对象得到的数据

• 从现象与时间关系来看

横截面数据（静态数据）：在同一时间对同一总体内不同单位的数量进行观察而获得的数据

时间序列数据（动态数据）：在不同时间对同一总体的数量表现进行观察而获得的数据

面板数据：同时在时间和横截面空间上取得的二维数据

• 数据的表现形式

绝对数、相对数、平均数

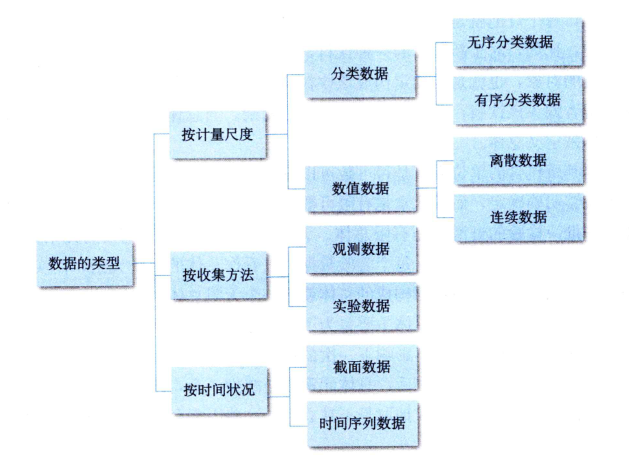
（3）总体、样本、参数、统计量和变量

统计总体：根据一定目的确定所要研究的事物的全体，是由客观存在的、具有某种相同性质的许多个别事物构成的整体

总体单位（简称单位）：组成总体的各个个体

根据单位数量，总体可以分为有限总体和无限总体

样本：从总体中抽取的一部分元素的集合

总体参数：描述统计特征的概括性数字度量

样本统计量：样本的函数，用来描述样本特征的概括性数字度量

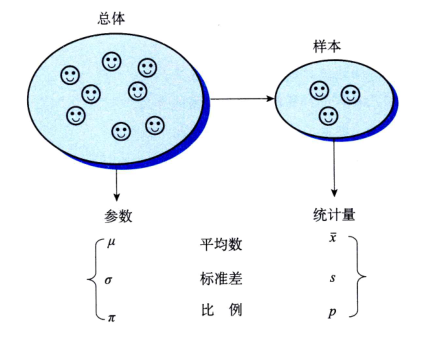
变量：说明现象某种特征的概念

• 分类变量
• 数值变量
  • 连续型变量：在数轴上取值连续不断的变量
  • 离散型变量：仅可通过计数获得的变量，通常取值为整数值

变量值：变量的具体取值

（4）一个案例

（5）数据的来源

数据主要可分为一手数据与二手数据

一手数据来源包括但不限于直接观察、统计调查、实验记录、人员采访等

二手数据来源包括但不限于统计年鉴、相关期刊、有关网站、数据库等

（6）概率抽样与非概率抽样

概率抽样：也称随机抽样，是指遵循随机原则进行的抽样，总体中每个单位都有一定的机会被选入样本。这个概率不一定要相等，但是是可计算的。（等概率抽样和不等概率抽样）

• 简单随机抽样：从包括总体 $N$ 个单位的抽样框中随机地、一个个地抽取 $n$ 个单位作为样本，每个单位的入样概率是相等的。（1948年的总统选举获胜的方法）
• 分层抽样
• 整群抽样
• 系统抽样
• 多阶段抽样

非概率抽样：抽取样本时不是依据随机原则，而是根据研究目的对数据的要求，采用某种方式从总体中抽出部分单位对其实施调查。

• 方便抽样
• 判断抽样
• 自愿样本（文学文摘的方式，曾经在1916年到1932年间成功预测当选的总统）
• 滚雪球抽样
• 配额抽样（盖洛普公司的方式，1936年的总统选举获胜的方法）

（7）抽样误差与非抽样误差

抽样误差：由抽样随机性引起的样本结果与总体真值之间的差异，是可计算的

非抽样误差：除了抽样误差外，由其他原因引起的样本观测结果与总体真值之间的差异

• 抽样框误差：抽样框不全或者抽样框未更新
• 回答误差
  • 理解误差
  • 记忆误差
  • 有意识误差
• 无回答误差
• 调查员误差
• 测量误差

（8）数据的预处理

1. 数据审核
2. 数据筛选
3. 数据排序

（9）分类数据的整理与图示

统计分组：根据统计研究的目的和客观现象的内在特点，按某个标志（或几个标志）把被研究的总体划分为若干个不同性质的组。统计分组的对象是总体。统计标志可以是品质标志，也可以是数量标志。

• 统计分组的种类

1. 按分组标志的多少：简单分组和复合分组
2. 按分组的标志性质不同：数量分组（定距尺度和定比尺度）和品质分组（定类尺度和定序尺度）

• 统计分组的原则：穷尽原则和互斥原则

• 品质分组的方法：需要制定一套标准的分类指引

• 数量分组的方法：

  1. 单项式分组和组距式分组

     1. 单项式分组（1、2、3、4）

     2. 组距式分组（1、2、3、4个及以上 或 100以下、100-200、200以上）

        组限：一组数据中上下限的距离，相邻两组的界限。

        1. 间断型组距分组（1、2、3、4个及以上）：组限不相连的数量分组方法
        2. 连续型组距分组（100以下、100-200、200以上）：组限相连的数量分组方法，一般要求左闭右开

  2. 等距分组和异距分组

• 斯特杰斯经验公式：$n = 1 + 3.3\lg N$，$d = R / n = (x_{max} - x_{min}) / (1 + 3.3 \lg N)$

• 统计数据的显示：统计表和统计图

（10）集中趋势的度量

• 平均数
  • 简单平均数
  • 加权平均数
  • 调和平均数
  • 几何平均数
• 中位数
• 分位数
• 众数

（11）离散程度的度量

• 全距
• 四分位距
• 方差和标准差
• 离散系数
• 标准分数（z-score）

（12）分布的形状

• 偏度系数

  $SK=\frac{n}{(n-1)(n-2)}\sum\left(\frac{x_i-\overline{x}}{s}\right)^3$

• 峰度系数

  $K=\frac{n(n+1)}{(n-1)(n-2)(n-3)}\sum\left(\frac{x_i-\overline{x}}{s}\right)^4-\frac{3(n-1)^2}{(n-2)(n-3)}$

2 统计量及抽样分布

（1）统计量的定义

（2）常用统计量

（3）抽样分布

• 样本均值分布：近似服从正态分布，$\overline{x} \overset{.}{\sim} N(\mu, \sigma ^2 / n)$

• 样本方差分布

• 样本比率分布

• 卡方分布：若 $X_1, X_2, \cdots , X_n$ 是独立同分布于正态总体 $N(\mu, \sigma^2)$ 的随机变量，且 $\chi^{2} = X_{1}^2 + X_{2}^2 + \cdots + X_{n}^2$，那么 $\chi^2 \sim \chi^2(n)$

  • $E(\chi^2) = n$
  • $D(\chi^2) = 2n$
  • $x_1, x_2, \cdots x_n$ 是来自正态总体 $N(\mu, \sigma^2)$ 的一个样本，$\overline{x}, s^2$ 分别是他们的均值和方差，则
    • $\overline{x}$ 和 $s^2$ 独立
    • $\overline{x} \sim N(\mu, \sigma^2/n)$，标准化后，$\frac{\overline{x} - \mu}{\sigma/\sqrt{n}} \sim N(0, 1)$
    • $\frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)$

• $t$ 分布：若$X_1 \sim N(0, 1), X_2 \sim \chi^2(n)$，那么 $t = \frac{X_1}{\sqrt{X_2/n}} \sim t(n)$

• 若$t \sim t(n)$，则$t^2 \sim F(1, n)$

  • $x_1, x_2, \cdots x_n$是来自正态总体$N(\mu, \sigma^2)$的一个样本，$\overline{x}, s^2$分别是他们的均值和方差，则有$t = \frac{\sqrt{n} (\overline{x} - \mu)}{s} = \frac{\overline{x} - \mu}{s/\sqrt{n}} \sim t(n-1)$ （注意变形）

  • $x_1, x_2, \cdots x_m$来自正态总体$N(\mu_1, \sigma_1^2)$，$y_1, y_2, \cdots y_n$来自正态总体$N(\mu_2, \sigma_2^2)$，如果总体中$\sigma_1 = \sigma_2 = \sigma$，那么样本中满足，$\frac{(\overline{x}-\overline{y})-(\mu_1 - \mu_2)}{s_w^2\sqrt{\frac{1}{m}+\frac{1}{n}}} \sim t(m + n -2)$，其中，$s_w$是两个样本的方差的加权平均，即

    $s_w=\frac{(m-1)s_x + (n-1)s_n}{m+n-2} = \frac{\sum\limits_{i=1}^{m}(x_i-\overline{{x}})^2 + \sum\limits_{i=1}^{n}(y_i-\overline{{y}})^2}{m+n-2}$

• $F$ 分布：若 $X_1 \sim \chi^2(m), X_2 \sim \chi^2(n)$ ，$F = \frac{X_1/m}{X_2/n}$，那么 $F \sim F(m, n)$

  • 服从$F$分布的随机变量的倒数依然服从$F$分布，$F \sim F(m, n), 1/F \sim F(n, m)$
  • $F_{\alpha}(m, n) = \frac{1}{F_{1-\alpha}(n, m)}$
  • $x_1, x_2, \cdots x_m$来自正态总体$N(\mu_1, \sigma_1^2)$，$y_1, y_2, \cdots y_n$来自正态总体$N(\mu_2, \sigma_2^2)$，那么有，$F = \frac{s_x^2/\sigma_1^2}{s_y^2/\sigma_2^2} \sim F(m-1, n-1)$（可以注意到，这个表达式与$\mu$无关）

3 参数估计

（1）基本概念

参数估计：用样本统计量去估计总体参数（基本原理）

估计量：用来估计参数的统计量（随机变量）

估计值：根据一个具体的样本估计出来的值（常数）

名词	概念
点估计	用样本一个统计量去估计总体未知参数（包括矩估计和极大似然估计）
区间估计	最后求出一个区间，这个区间包含真实值的概率称为置信水平
矩估计	点估计的一种，用样本的中心距或者原点矩替换总体的中心距或者原点矩
极大似然估计	点估计的一种，假装抽到了最有可能的结果，调整参数 $\theta$ 让这组样本被抽到的可能性（似然函数$L(\theta)$）最大
预测区间估计	对预测值的区间估计
无偏性/无偏估计	最终估计量的期望 $E(\hat{\theta})$ 等于实际值 $\theta$ ，估计值围绕着实际值上下波动，没有系统误差
有效性	在无偏性的基础上，减小波动的幅度（方差），越小越有效
一致性/相合性/相合估计	当样本量足够大的时候，估计值朝着真实值接近，则称为相合估计
均方误差$MSE$	$E(\hat{\theta}-\theta)^2=Var(\hat{\theta})+(E\hat{\theta}-\theta)^2$ 前面方差衡量有效性，后面距离中心平方衡量无偏性

点估计：$x_1, x_2, \cdots , x_n$ 是来自总体的一个样本，总体中含有未知参数 $\theta$，那么利用样本的一个统计量 $\hat{\theta}=\hat{\theta}(x_1, x_2, \cdots , x_n)$ 来估计总体未知参数 $\theta$ 的方法叫做点估计。

• 矩估计：总体的密度函数为 $p(x; \theta_1, \theta_2, \cdots, \theta_n)$（如果总体中含有未知参数，通常我们把它表现在总体的密度函数里），总体的 1 到 $k$ 阶原点矩（中心距也行）为 $u_1, u_2, \cdots, u_n$。从中抽出一个样本 $x_1, x_2, \cdots , x_n$，记这个样本的 1 到 $k$ 阶原点矩（中心距也行的）为 $a_1, a_2, \cdots, a_n$。如果 $\theta$ 可以表示为总体矩的函数，即 $\theta=\theta(u_1, u_2, \cdots, u_n)$，那么我们用样本矩来替换总体矩，即 $\hat{\theta}=\theta(a_1, a_2, \cdots, a_n)$，得到的结果 $\hat{\theta}$ 称为参数 $\theta$ 的矩估计
• 极大似然估计：设总体概率密度函数为 $p(x;\theta)$，$\theta \in \Theta$，$x_1, x_2, \cdots , x_n$ 是来自总体的一个样本，将样本的联合概率函数看成 $\theta$ 的函数，用 $L(x_1, x_2, \cdots , x_n; \theta)$ 表示，记为 $L(\theta)$，若统计量满足：$L(\hat{\theta}) = \underset{\theta \in \Theta}{\max} L(\theta)$，则称 $\hat{\theta}$ 称为参数 $\theta$ 的极大似然估计

区间估计：设 $\theta$ 是总体的一个参数，其参数空间为 $\Theta$, $x_1, \cdots, x_n$ 是来自该总体的样本。对给定的一个 $\alpha$ (0 < $\alpha$ < 1)，假设有两个统计量 $\hat{\theta}_L = \hat{\theta}_L(x_1, \cdots, x_n)$ 和 $\hat{\theta}_U = \hat{\theta}_U(x_1, \cdots, x_n)$，若对任意的 $\theta \in \Theta$，有 $ P_\theta(\hat{\theta}_L \leqslant \theta \leqslant \hat{\theta}_U) \geqslant 1 - \alpha $，则称随机区间 $[\hat{\theta}_L, \hat{\theta}_U]$ 为 $\theta$ 的置信水平为 $1-\alpha$ 的置信区间，或简称 $[\hat{\theta}_L, \hat{\theta}_U]$ 是 $\theta$ 的 $1-\alpha$ 置信区间。$\hat{\theta}_L$ 和 $\hat{\theta}_U$ 分别称为 $\theta$ 的（双侧）置信下限和置信上限。

置信水平 $1 - \alpha$ 有一个频率解释：在大量重复使用 $\theta$ 的置信区间 $[\hat{\theta}_L, \hat{\theta}_U]$ 时，每次得到的样本观测值是不同的，从而每次得到的区间也是不一样的。对一次具体的观测值而言，$\theta$ 可能在 $[\hat{\theta}_L, \hat{\theta}_U]$ 内，也可能不在。平均而言，在这大量的区间估计观测值中，至少有 $100(1 - \alpha)%$ 包含 $\theta$。

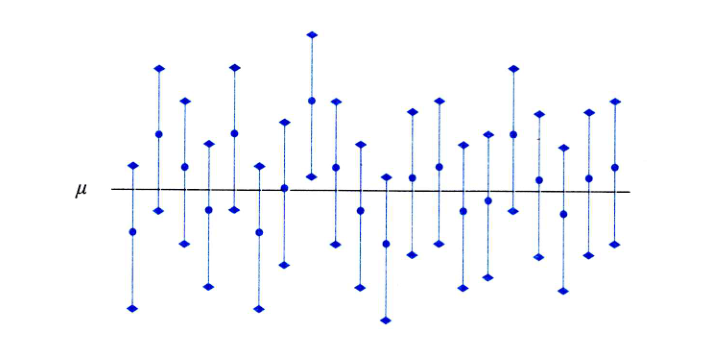
（2）评价指标

• 无偏性：$E(\hat{\theta}) = \theta$
• 有效性：若 $\hat{\theta}_1,\hat{\theta}_2$ 是 $\theta$ 的两个无偏估计，那么若 $Var(\hat{\theta}_1) < Var(\hat{\theta}_2)$，我们称 $\hat{\theta}_1$ 比 $\hat{\theta}_2$ 有效
• 一致性（相合性）：设 $\theta \in \Theta$，$\hat{\theta} = \hat{\theta}_n(x_1, x_2, \cdots, x_n)$ 是 $\theta$ 的一个估计量，$n$ 是样本容量，如果 $\forall \varepsilon>0$，当 $n\rightarrow\infty$ 时，总有 $\underset{n\rightarrow\infty}{\lim}P(|\hat{\theta}-\theta|\geq \epsilon)=0$，那么称 $\hat{\theta}$ 是 $\theta$ 的相合估计

（3）常见的参数估计

id	待估参数	条件	枢轴量
1	单个正态总体 $\mu$	$\sigma$ 已知	$G=\frac{\overline{x}-\mu}{\sigma/\sqrt{n}} \sim N(0, 1)$
2	单个正态总体 $\mu$	$\sigma$ 未知	$G=\frac{\overline{x}-\mu}{s/\sqrt{n}} \sim t(n - 1)$，OLS
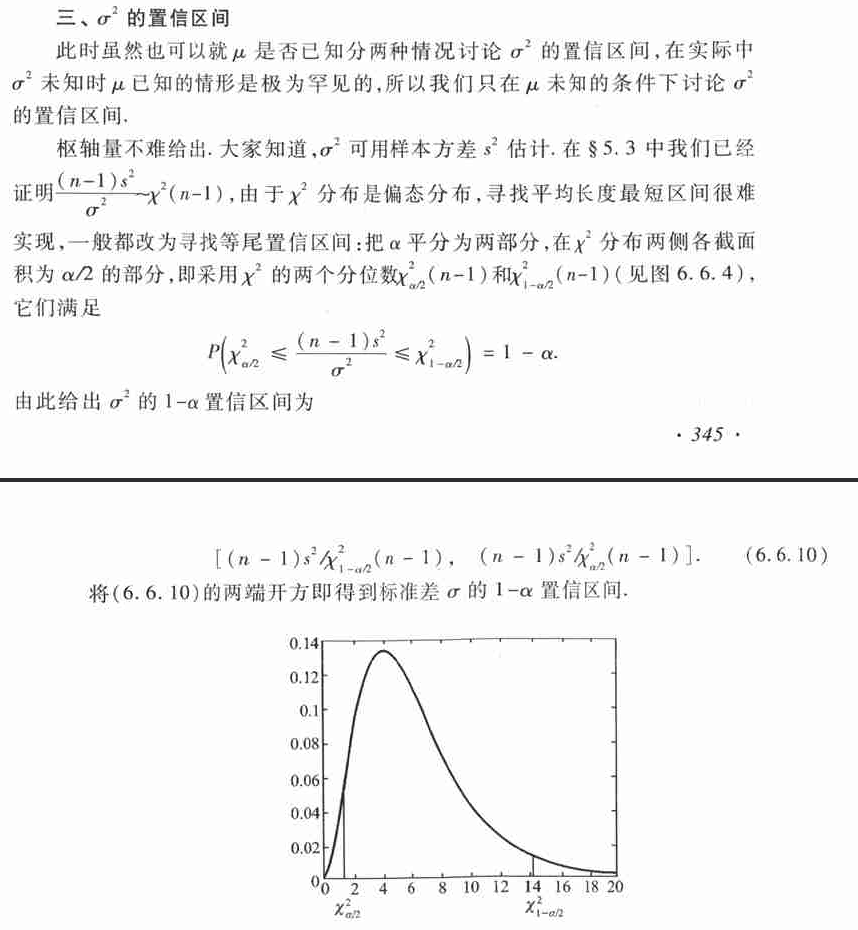
3	单个正态总体 $\sigma^2$	$\mu$ 未知	$G=\frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)$
4	二点分布 $p$	大样本，$X \sim b(1, p)$	$G=\frac{\overline{x}-p}{\sqrt{p(1-p)/n}} \overset{.}{\sim} N(0, 1)$
5	两个独立正态总体$\mu_1 - \mu_2$	$\sigma_1, \sigma_2$ 已知	$G = \frac{\overline{x} - \overline{y} - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{m} + \frac{\sigma_2^2}{n}}} \sim N(0, 1)$
6	两个独立正态总体$\mu_1 - \mu_2$	$\sigma_1=\sigma_2=\sigma = ?$	$G = \sqrt {\frac{{mn(m + n - 2)}}{{m + n}}} \frac{{\bar x - \bar y - ({\mu _1} - {\mu _2})}}{{\sqrt {(m - 1)s_x^2 + (n - 1)s_y^2} }} \sim t(m+n-2)$
7	两个独立正态总体$\mu_1 - \mu_2$	$\sigma_1/\sigma_2=c$	$G = \sqrt {\frac{{mn(m + n - 2)}}{{mc + n}}} \frac{{\bar x - \bar y - ({\mu _1} - {\mu _2})}}{{\sqrt {(m - 1)s_x^2 + (n - 1)s_y^2/c} }} \sim t(m+n-2)$
8	两个独立正态总体$\mu_1 - \mu_2$	$\sigma_1, \sigma_2$ 没啥信息，但是 $m, n$ 很大	$G = \frac{\overline{x} - \overline{y} - (\mu_1 - \mu_2)}{\sqrt{\frac{s_1^2}{m} + \frac{s_2^2}{n}}} \overset{.}{\sim} N(0, 1)$
9	两个独立正态总体$\mu_1 - \mu_2$	$\sigma_1, \sigma_2$ 没啥信息， $m, n$ 也很小	$G = \frac{\overline{x} - \overline{y} - (\mu_1 - \mu_2)}{s_0} \overset{.}{\sim} t(l), s_0=\sqrt{\frac{s_x^2}{m}+\frac{s_y^2}{n}}, l=s_0^4 / \left(\frac{s_x^4}{m^2(m-1)}+\frac{s_y^4}{n^2(n-1)} \right)$
10	两个独立正态总体$\sigma_1^2/\sigma_2^2$	无	$G = \frac{s_x^2/\sigma_1^2}{s_y^2/\sigma_2^2} \sim F(m-1, n-1)$

估计思路（id 排序）：

1. 通过已有样本的分布 $\overline{x} \sim N(\mu, \sigma^2)$ 进行标准化得到
2. $\sigma$ 未知，应该用 $s$ 去替代 $\sigma$ ，得到的分布是 $t$ 分布，$\frac{\overline{x}-\mu}{s/\sqrt{n}} \sim t(n - 1)$
3. 涉及到方差的，单正态总体卡方分布，两正态总体 $F$ 分布，此处卡方分布。利用性质，$\frac{(n-1)s^2}{\sigma^2}\sim \chi^2(n-1)$
4. 此处是由中心极限定理得到的，二点分布样本均值服从如下分布，$\overline{x} \sim N(p, \frac{p(1-p)}{n})$，标准化即可
5. 因为独立，所以有，$\overline{x} - \overline{y} \sim N(\mu_1 - \mu_2, \sigma_1^2/m+\sigma_2^2/n)$，标准化即可
6. 因为独立，所以有，$\overline{x} - \overline{y} \sim N(\mu_1 - \mu_2, (1/m+1/n)\sigma^2)$，标准化之后是有$\sigma$的，但是通过下式，$\frac{(m-1)s_x^2}{\sigma^2}+ \frac{(n-1)s_y^2}{\sigma^2} =\frac{(m-1)s_x^2+(n-1)s_y^2}{\sigma^2}\sim \chi^2(m+n-2)$（卡方分布的可加性），将方差进行替换，得到一个 $t$ 分布（ $t$ 分布是标准正态分布除以根号下卡方分布除以自由度）
7. 构造思路同上，最后保留 $\sigma_1$，$\frac{(m-1)s_x^2+(n-1)s_y^2/c}{\sigma_1^2}\sim \chi^2(m+n-2)$，然后操作同上
8. 因为基本上任何分布，样本量足够大的时候都朝着正态分布趋近
9. 死记硬背吧，这个还在研究中
10. 两个卡方分布变量$\frac{(m-1)s_x^2}{\sigma_1^2}\sim \chi^2(m-1)$、$\frac{(n-1)s_y^2}{\sigma_2^2}\sim \chi^2(n-1)$除以各自的自由度（$m-1$和$n-1$）后再相除是$F$分布

（4）正态总体参数的区间估计

• 一

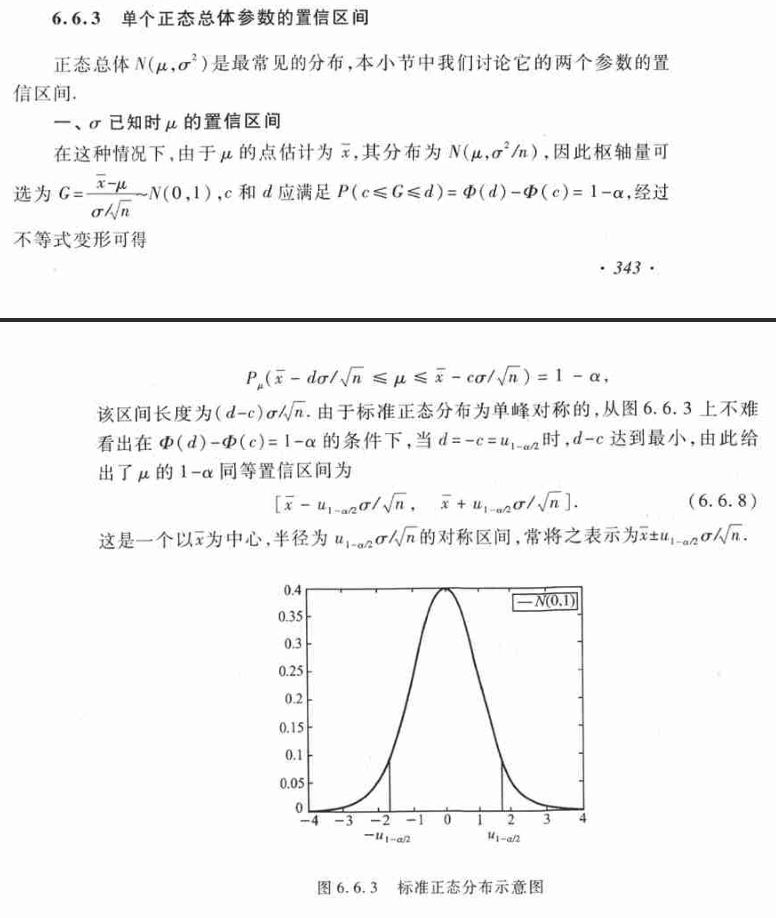
• 二

• 三

4 假设检验

假设检验的基本原理源于“小概率事件”原理,是一种基于概率性质的反证法，其核心思想是小概率事件在一次试验中几乎不会发生。

（1）概念及基本步骤

假设检验：针对总体参数提出一个假设，然后通过样本统计量进行检验

基本步骤：

• 建立假设（$H_0$ 和 $H_1$）

  我们通常把无影响、没效果作为 $H_0$（除非有足够的理由证明发生了变化），$H_0$ 和 $H_1$都是基于总体参数的，而不是样本。思想是，通过样本检验总体假设是否正确。

• 选择检验统计量并给出拒绝域形式

  参照区间估计枢轴量表格即可，要注意的是，检验统计量和枢轴量不同，检验统计量要把枢轴量里面的参数替换成检验值。比如说，在一次检验中，$H_0: \mu_1 = \mu_2$，选择枢轴量为$G = \frac{\overline{x} - \overline{y} - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{m} + \frac{\sigma_2^2}{n}}} \sim N(0, 1)$ ，对应的检验统计量为$u = \frac{\overline{x} - \overline{y}}{\sqrt{\frac{\sigma_1^2}{m} + \frac{\sigma_2^2}{n}}} \sim N(0, 1)$ ，其实就是说检验统计量不含有未知参数，必须是一个可以用样本计算的数。拒绝域的形式和备择假设方向一致，

原假设	备择假设	拒绝域形式
$\mu_1 = \mu_2$	$\mu_1 \not= \mu_2$	$|u| \geq u_0$
$\mu \geq \mu_0$	$\mu < \mu_0$	$u \leq u_0$
…	…	…

• 选择显著性水平，给出拒绝域

  确定了拒绝域 $W$ 的方向后，选择相应的显著性水平找出用于判断的临界值。常用的是 $\alpha=0.05$

• 作出判断，判断检验统计量是否在拒绝域内

（2）小概率事件的基本原理

进行假设检验利用的是小概率原理，小概率原理是指发生概率很小的随机事件在一次试验中几乎不可能发生，但多次重复实验后必然发生。根据这一原理可以作出是否拒绝原假设的决定。但什么样的概率才算小呢？著名的英国统计学家费希尔把小概率的标准定为0.05，虽然费希尔并没有对为什么选择0.05给出充分的解释，但人们还是沿用了这个标准，把 0.05或比0.05更小的概率看成小概率。

（3）两类错误

第 Ⅰ 类错误（$\alpha$ 错误，弃真错误）：原假设为真，但是被拒绝

第 Ⅱ 类错误（$\beta$ 错误，取伪错误）：原假设为伪，但没被拒绝

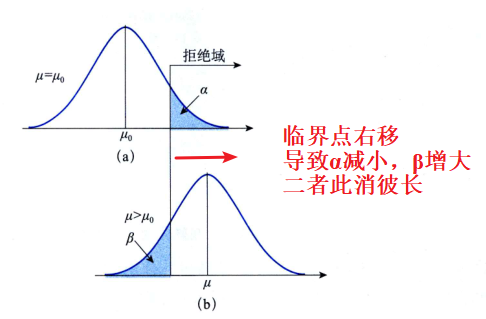
注：这里 $\mu_0$ 是假设参数值。（a）是假设的统计量分布，（b）是实际的统计量分布。

（1）当 $H_0: \mu = \mu_0$ 为真时，如果 $\mu$ 落入 $\alpha$ 区域，那么就会出现第一类错误，拒绝了正确的假设，想要降低需要选择比较低的显著性水平 $\alpha$

（2）当 $H_0: \mu = \mu_0$ 为伪时，比如实际上 $\mu > \mu_0$，但是观测 $\mu$ 落入了 $\beta$ 区域，那么就会出现第二类错误，接受了错误的假设，想要降低需要选择比较低的 $\beta$ 水平

第一类错误的概率就是最初假设的显著性水平：$\alpha$

第二类错误的概率需要计算，以上图为例，第二类错误的概率是 $\mu$ 落入两条粉色线条中间区域的概率

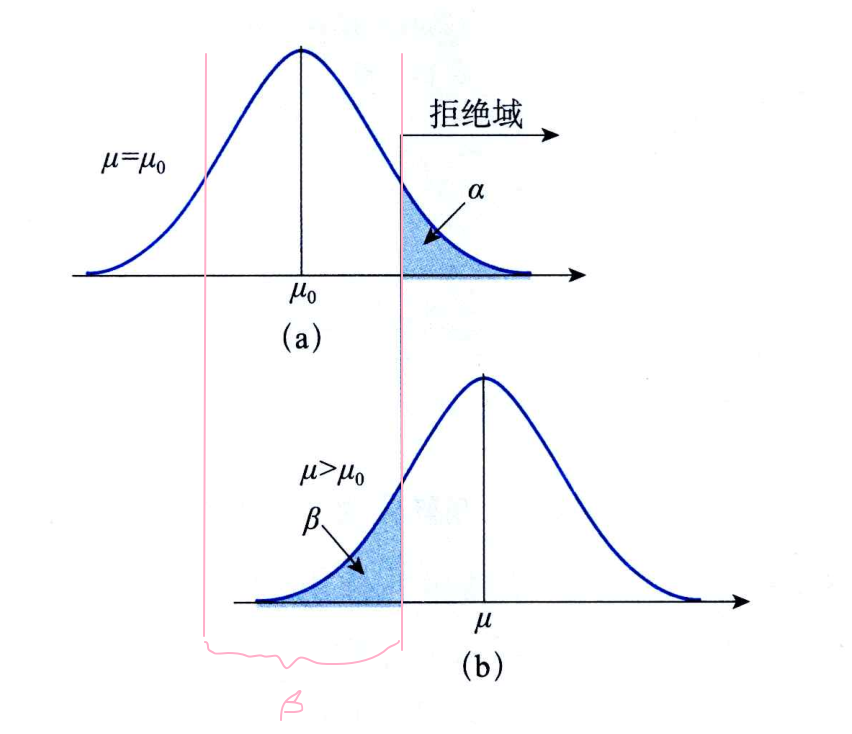
• $\alpha$ 与 $\beta$ 是在两个前提下的概率，所以 $\alpha + \beta$ 不一定等于 1

• 在其他条件不变的情况下，$\alpha$ 与 $\beta$ 不能同时增加或减少

• 样本量的增加能够在给定 $\alpha$ 时减小 $\beta$

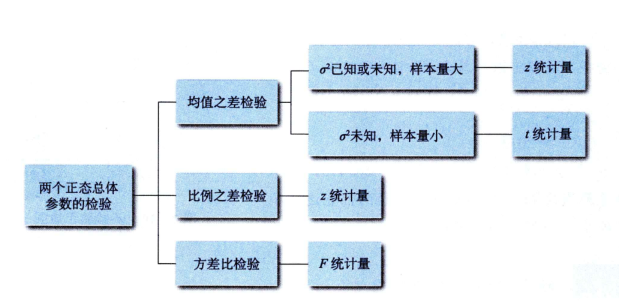
（4）正态总体检验

• 均值检验：用 $z$ 统计量（已知方差）或者 $t$ 统计量（未知方差）

• 方差检验：用 $\chi^2$ 统计量，$\frac{(n-1)s^2}{\sigma^2} \sim \chi^2(n-1)$

• 两个正态总体（参考参数估计章节）

  

（5）分布拟合检验

用于测定两个分类变量的相关程度，用于检验样本数据是否来自某个特定的概率分布。

$\chi^2 = \sum\limits_{i=1}^n \frac{(f_{i,0} - f_{i,e})^2}{f_{i,e}} \sim \chi^2(n-1)$

5 相关分析与回归分析

（1）相关分析

• 相关图
• 相关系数
  • 皮尔逊相关系数：$r = \frac{\sum(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum(x_i - \bar{x})^2\sum(y_i - \bar{y})^2}}$
  • 相关系数的 $t$ 值：$t = \frac{r \sqrt{n-2}}{\sqrt{1 - r^2}} \sim t(n-2)$
  • 斯皮尔曼相关系数：$r_s=1-\frac{6\sum_{i=1}^nd_i^2}{n(n^2-1)}$，$d_i$ 代表等级差

（2）回归分析

• 回归形式：

  • 一元：$Y_{i} = \beta_0 + \beta_1 X_i + \varepsilon_{i}$

    

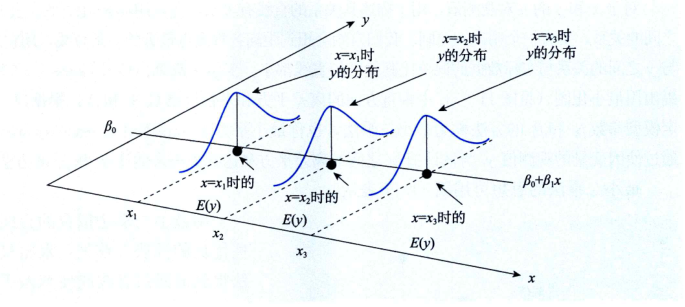
  • 假设

    • 模型正确设立，总体回归模型是线性的
    • 严格外生性：$\mathbb{E}(\varepsilon_i|{\bf{X}}) = 0$
    • 不存在严格多重共线性，数据矩阵列满秩，$\mathrm{rank}({\bf{X}}) = m$
    • 球型干扰项，即 $Var(\varepsilon_i | {\bf{X}}) = \mathbb{E}(\varepsilon_i^2 | {\bf{X}}) = \sigma^2$，$cov(\varepsilon_i,\varepsilon_j) = \mathbb{E}(\varepsilon_i\varepsilon_j) = 0,i\not=j$

  • 推论

    • $\mathbb{E}(\varepsilon_i) = 0$
    • $cov(X_i, \varepsilon_j) = \mathbb{E}(X_i\varepsilon_j) = 0$
    • $Var(\varepsilon_i) = \sigma^2$，用到方差分解原理：$\mathrm{Var}(\varepsilon)=\mathbb{E}[\mathrm{Var}(\varepsilon|X)]+\mathrm{Var}[\mathbb{E}(\varepsilon|X)]$

• 最小二乘估计原理：最小化观测值与估计值的残差平方和

• 最小二乘参数估计方法

  • 点估计

    

  • 极大似然估计：最后发现依然是最小化残差平方和

  • 矩估计：

    • 两个条件
      • $\mathbb{E}(\varepsilon_i) = 0$
      • $cov(X_i, \varepsilon_i) = \mathbb{E}(X_i\varepsilon_i) = 0$
    • 对应的矩条件
      • $\frac{1}{n} \sum (\hat{Y} - \hat{\beta}_0-\hat{\beta}_1X_i) = 0$
      • $\frac{1}{n} \sum (\hat{Y} - \hat{\beta}_0-\hat{\beta}_1X_i)X_i = 0$

  • 矩阵推导

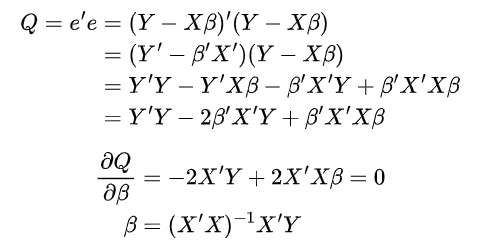
常见的矩阵求导公式：

1. 线性函数导数

$$
\frac{\partial {\bf{a}}’{\bf{x}}}{\partial {\bf{x}}} = {\bf{a}}
$$

$$
\frac{\partial {\bf{A}}{\bf{x}}}{\partial {\bf{x}}} = {\bf{A}}
$$

2. 二次型导数

$$
\frac{\partial {\bf{x}}’{\bf{A}}{\bf{x}}}{\partial {\bf{x}}} = ({\bf{A}} + {\bf{A}}’){\bf{x}}
$$

3. 矩阵的迹

$$
\frac{\partial \mathrm{tr}(\bf{AX})}{\partial {\bf{X}}} = {\bf{A}}’
$$

4. 行列式导数

$$
\frac{\partial \det({\bf{X}})}{\partial {\bf{X}}} = \det({\bf{X}})({\bf{X}}^{-1})’
$$

5. 对矩阵求导

$$
\frac{\partial \bf{a}’{\bf{X}}{\bf{X}}’{\bf{b}}}{\partial {\bf{X}}} = \frac{\partial \bf{a}’{\bf{X}}’{\bf{X}}{\bf{b}}}{\partial {\bf{X}}} = ({\bf{a}}{\bf{b}}’ + {\bf{b}}{\bf{a}}’)X
$$

• 估计量的性质

  • BLUE（最佳线性无偏估计）：线性性（$\beta$ 是 $Y_i$ 的线性组合）、无偏性（$\mathbb{E}(\hat{\beta} | X) = \beta$）、有效性（方差最小）

  • 一元回归表达式：

    • $\hat{\beta}_1 = \sum k_iy_i = \beta_1 + \frac{\sum x_i\varepsilon_i}{\sum x_i^2}$
    • $\hat{\beta}_0 = \sum w_iy_i = \beta_0 + \sum(1/n + \bar x k_i)\varepsilon_i$
    • 矩阵形式：$\hat{\beta} = \beta + \mathbb{E}((X’X)^{-1}X’\varepsilon)$

  • 期望、方差及其分布

    • $\hat{\beta}_1 \sim N\left( \beta_1, \frac{1}{\sum (x_i - \bar{x})^2} \sigma^2 \right)$

    • $\hat{\beta}_0 \sim N\left( \beta_0, \left( 1/n + \frac{\bar{x}^2}{\sum (x_i - \bar{x})^2} \right) \sigma^2 \right)$

    • $\hat{\beta} \sim N(\beta, \sigma^2(X’X)^{-1})$

      

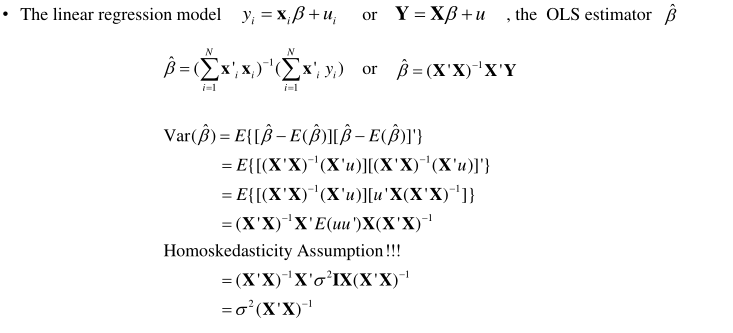
• 三个差平方和：SST = SSR + SSE

名称	形式
总离差平方和：SST	$\sum (y_i - \bar{y})^2$
回归平方和：SSR	$\sum (\hat{y} - \bar{y})^2$
残差平方和：SSE	$\sum (y_i - \hat{y})^2$

• 拟合优度：$R^2 = \frac{SSR}{SST}$

• 显著性检验

  • 回归系数的显著性检验：$t$ 检验，$\frac{\hat{\beta}}{se(\hat{\beta})} \sim t(n-k)$
  • 方程的显著性检验：$F$ 检验，$\frac{SSR / (k-1)}{SSE / (n - k)} \ \sim F(k-1, n-k)$

• 预测误差

  • $S_e = \sqrt{\frac{\sum (y_i - \hat{y})^2}{n - k}} = \sqrt{\frac{SSE}{n-k}}$
  • $\hat{Y}_i \sim \left(\beta_0 + \beta_1 X_i, \left( 1/n + \frac{(x_i - \bar{x})^2}{\sum (x_i - \bar{x})^2} \right) \sigma^2 \right)$
  • 置信区间：$\hat{y}_i \pm t_{\alpha / 2} \left( 1/n + \frac{(x_i - \bar{x})^2}{\sum (x_i - \bar{x})^2} \right) S_e $ ，可以得到 $\mathbb{E}(y_i)$ 对应的置信区间
  • 也有一些学者认为是 $\hat{y}_i \pm t_{\alpha / 2} \left(1 + 1/n + \frac{(x_i - \bar{x})^2}{\sum (x_i - \bar{x})^2} \right) S_e $

（3）模型诊断

• 多重共线性

  • 后果

    • 参数估计量不存在：因为矩阵列不满秩，导致 $X’X$ 不可逆

    • 估计量方差变大。当 $x_1, x_2$ 存在部分共线性时，方差膨胀因子为：

      $\mathrm{VIF}(\hat{\beta}_1) = 1 / \left(1-\frac{(\sum x_{i1}x_{i2})^{2}}{\sum x_{i1}^{2}\sum x_{i2}^{2}} \right) = 1 / (1 - r_{12}^2)$

    • 参数估计量经济意义不合理：因为无法分离二者关系

    • 变量显著性检验和模型预测功能失去意义：方差变大，导致 $t$ 值变小和预测区间变大

  • 检验方法

    • 相关系数矩阵：看一下解释变量之间的相关系数是否趋于 1
    • 综合统计检验法：如果模型的 $R^2$ 和 $F$ 值较大，但是每个系数的 $t$ 值都比较小，说明联合显著，但是共线性的存在使得他们对 $Y$ 的独立作用无法分辨
    • 判定系数法：使用变量 $x_j$ 对其他变量回归，作 $F$ 检验：$F_j = \frac{R_j^2 / (k - 1)}{(1 - R_j^2) / (n - k)} \sim F(k - 1, n - k)$，或者看 VIF 值，$\mathrm{VIF} = \frac{1}{1 - R_j^2}$，一般认为 VIF 大于 10 时存在严重的多重共线性问题
    • 逐步回归法：逐个引入新变量，看 $R^2$ 的变化是否显著

  • 解决方法

    • 逐步回归剔除
    • LASSO 回归
    • 岭回归
    • 弹性网
    • 主成分分析等方法降维

• 异方差问题

  • 后果

    • 参数估计量非有效：虽然仍然具有线性性与无偏性，但是不再具备有效性。即使是大样本晴空下，也不具有渐进有效性
    • 变量的显著性检验失去意义：估计量方差发生变化，导致分布变化
    • 模型预测失效

  • 检验方法

    • 图示法：使用残差平方与 $X$ 的图像分析

    • BP 检验：使用残差平方对 $X$ 回归，作 $F$ 或 $\chi^2$ 检验：

      $F = \frac{R_{e^2}^2 / (k - 1)}{(1 - R_{e^2}^2) / (n - k)} \sim F(k - 1, n - k)$

      $LM = n \cdot R^2_{e^2} \sim \chi^2(k - 1)$

    • 怀特检验：类似 BP 检验，但是在回归时加入平方项和交互项

  • 解决方法

    • 加权最小二乘法
    • 异方差稳健标准误
    • 聚类稳健标准误
    • Driscoll-Kraay 标准误
    • Newey-West 回归

• 内生性问题

  • 后果

    • 参数估计量有偏、不一致且非有效（小样本有偏，大样本不一致）
    • 变量显著性检验和模型预测功能失去意义

  • 检验方法

    • 豪斯曼检验

      

    • 过度识别检验（如 Sargan 检验和 Hansen 检验，在使用多个工具变量，检验该组工具变量的外生性）

  • 解决方法

    • 增加控制变量：缓解遗漏变量问题
    • PSM、熵平衡、Heckman方法：缓解选择性偏误
    • 工具变量法：缓解上述一系列问题和反向因果等
    • Oster 检验：验证遗漏因素对核心解释变量的影响不足以推翻原有结论

• 模型设定偏误

  • 影响

    • 参数估计量有偏、不一致且非有效（小样本有偏，大样本不一致）
    • 方程不具有经济意义
    • 变量显著性检验和模型预测功能失去意义

  • 检验方法

    • 检验是否包含无关变量：$t$ 检验

    • 检验是否存在相关的遗漏变量：残差与 $X$ 的图示

    • 一般性设定偏误检验：RESET 检验

      

  • 解决方法

    • 增加潜在的遗漏变量
    • 更换模型形式，比如采用非线性模型

6 时间序列分析

（1）时间序列分析概述

时间序列是把同一现象在不同时间上的观察数据按时间先后顺序排列起来所形成的数列，也称动态数列。

• 时间序列的编制原则：

  • 时间一致：分隔一致

  • 总体范围一致

  • 经济内容、计算口径和计算方法一致

（2）时间序列的水平分析与速度分析

• 水平分析

  • 平均值：不同时点上的数据求平均值
  • 增长量与平均增长量：包括逐期增量、累计增量、同比增量、平均增量

• 速度分析

  • 发展速度：报告期水平 / 基期水平
    • 环比发展速度（逐期发展速度）
    • 定基发展速度（发展总速度）
  • 增长速度：发展速度 - 1
  • 平均发展速度和平均增长速度

（3）长期趋势和季节变动的测定

• 时间序列的构成

  • 长期趋势 $T$
  • 季节变动（一年内所呈现的较有规律的周期性起伏波动） $S$
  • 循环变动（较长时间内呈现的涨落相同、峰谷交替的周期性波动） $C$
  • 不规则变动 $I$

• 时间序列的分解

  • 加法模型：$Y_t = T_t + S_t + C_t + I_t$
  • 乘法模型：$Y_t = T_t \times S_t \times C_t \times I_t$

• 长期趋势的测定方法

  • 时距扩大法：通过合并消除掉季节波动和抵消不规则变动
  • 移动平均法
  • 趋势方程拟合法：线性趋势、非线性趋势

• 季节变动的测定

  • 同期平均法：不同年份同个季度求平均
  • 移动平均趋势剔除法
    • 用移动平均值作为长期趋势值
    • 用时间序列值减去或除以对应的长期趋势值
    • 同期平均
    • 调整指数：归一化处理

• 计量手段：滤波器或平滑方法提取趋势与周期性成分：BK滤波器、HP滤波器、HW平滑法等